Traitement du langage : Comment comprendre le sens d'une question ?
Quand on recherche une information précise dans de larges volumes de textes, on a tendance a fonctionner par mots clés : Par exemple, dans un text traitant de la littérature fraçaise, si on cherche le nom de l’auteur des Misérables, on peut chercher à l’interieur de ce texte des termes susceptibles d’être à proximité de la réponse cherchée : “Misérables auteur” ou “Misérables écrivain”.
Mais certains moteurs de recherche sont capables d’interpréter des questions posées en langage naturel. Par exemple, si on tape dans la barre de recherche Google “Qui a écrit les misérables ?”, l’algorithme est en mesure de détecter que l’entité recherchée est un auteur, sans que le mot “auteur“ soit explicitement présent :
Comment ces algorithmes arrivent-ils à saisir le sens d’une question, et à savoir quel type d’information est recherchée ? On se propose ici de construire un programme avec le but suivant : Pour une question donnée, on veut trouver quelle est l’entité cherchée (un lieu ? une durée ? une distance ? une personne ?)
Une approche naïve : construire “à la main” des champs lexicaux
La première idée qui pourrait nous venir en tête serait de définir des règles basées sur les champs lexicaux des mots de la question : par exemple, si celle-ci contient une des déclinaisons des verbes “écrire”, “rédiger”, elle a de grandes chances de porter sur un auteur. Comment généraliser cette idée et proposer un champ lexical pertient pour chaque catégorie de question?
On peut, pour commencer, définir clairement les catégories dans lesquelles on va classer les questions. Pour ça, on va utiliser un jeu de données pré-existant contenant 5452 questions, la base TREC, pour Text REtrieval Conference. Chaque question, en anglais, est classée parmi 6 catégories (Abbreviation, Description and abstract concepts, Entities, Human beings, Locations et Numeric values) et 50 sous-catégories, dont nous pouvons retrouver le détail ici.
Regardons d’abord à quoi ressemble notre jeu de données :
#On extrait la table du fichier csv gràce à la librairie pandas
import pandas as pd
data = pd.read_csv('/media/tidiane/D:/Dev/NLP/data/Question_Classification_Dataset.csv', encoding='latin-1')
data
| Questions | Category0 | Category1 | Category2 | |
|---|---|---|---|---|
| 0 | How did serfdom develop in and then leave Russ… | DESCRIPTION | DESC | manner |
| 1 | What films featured the character Popeye Doyle ? | ENTITY | ENTY | cremat |
| … | … | … | … | … |
| 5447 | What ‘s the shape of a camel ‘s spine ? | ENTITY | ENTY | other |
| 5448 | What type of currency is used in China ? | ENTITY | ENTY | currency |
| 5449 | What is the temperature today ? | NUMERIC | NUM | temp |
| 5450 | What is the temperature for cooking ? | NUMERIC | NUM | temp |
| 5451 | What currency is used in Australia ? | ENTITY | ENTY | currency |
Dans chaque catégorie, nous pouvons voir quels mots sont les plus utilisés : Ceux-ci sont les plus susceptibles de former un champ lexical cohérent.
#On groupe les questions par catégorie 2 :
data_group = data.groupby(['Category2'])['Questions'].apply(lambda x: ' '.join(x)).reset_index()
#On transforme ensuite nos questions aggrégées en dictionnaire contenant la fréquence de chaque mot :
def word_count(str):
counts = dict()
words = str.split()
for word in words:
if word in counts:
counts[word] += 1
else:
counts[word] = 1
counts = dict(sorted(counts.items(), key=lambda item: item[1], reverse=True))
return counts
data_group['count'] = data_group['Questions'].apply(word_count)
# Enfin, on affiche les 10 mots les plus fréquents de chaque catégorie :
for i in range(len(data_group)) :
print(data_group.loc[i, "Category2"])
count = data_group.loc[i, "count"]
print(list(count.keys())[0:10], "\n")

Les 10 termes apparaissant le plus souvent dans chaque catégorie
Tirer profit de la fréquence d’apparition des mots : l’inférence bayésienne
On va, à partir de ces champs lexicaux créés, construire un classificateur de questions, à partir de la méthode bayésienne. L’idée est simple : On va calculer les probabilités d’appartenance à chaque catégorie pour chaque mot , puis généraliser ces probabilités au niveau des phrases.
Imaginons pour le moment que notre base de données se composent uniquement de 3 questions, chacune dans une catégorie différente :
–How many departments are there in France ? (count)
–Who is the current french president ? (ind)
–When did french people rebel against their king ? (date)
On va d’abord lister la fréquence d’apparition de chaque terme dans chaque catégorie :
| count | ind | date | |
|---|---|---|---|
| against | 0 | 0 | 1 |
| are | 1 | 0 | 0 |
| current | 0 | 1 | 0 |
| departments | 1 | 0 | 0 |
| did | 0 | 0 | 1 |
| France | 1 | 0 | 0 |
| french | 0 | 1 | 1 |
| How | 1 | 0 | 0 |
| in | 1 | 0 | 0 |
| is | 0 | 1 | 0 |
| king | 0 | 0 | 1 |
| many | 1 | 0 | 0 |
| people | 0 | 0 | 1 |
| president | 0 | 1 | 0 |
| rebel | 0 | 0 | 1 |
| the | 0 | 1 | 0 |
| their | 0 | 0 | 1 |
| there | 1 | 0 | 0 |
| When | 0 | 0 | 1 |
| Who | 0 | 1 | 0 |
Voici une 4e phrase : How many people live in France ?
Pouvons nous savoir, à partir de nos trois phrases précédentes, à quelle catégorie celle-ci appartient ?
Essayons par exemple de calculer la probabilité que notre phrase appartienne à la catégorie count, sachant qu’elle contient les mots “How many people are in France”. On va noter cette probabilité $P(count/”How\ many\ people\ are\ in\ France”)$
Le théorème de Bayes nous permet d’écrire l’équation suivante :
$P(count/”How\ many\ people\ are\ in\ France”) = \frac{P(“How\ many\ people\ are\ in\ France”/count) * P(count)}{P(“How\ many\ people\ are\ in\ France”)} $
Comment calculer la probabilité $P(“How\ many\ people\ are\ in\ France”/count)$, c’est-à-dire la probabilité de tomber sur cette phrase exacte lorsqu’on tire une phrase dans la catégorie count au hasard ?
Notre jeu de données est bien trop réduit pour obtenir directement cette probabilité. On fait alors l’hypothèse simplificatrice que les apparitions individuelles des mots sont des événements indépendants entre eux. On peut alors décomposer la probabilité comme suivant:
$P(“How\ many\ people\ are\ in\ France”/count) = P(“How”/count) * P(“many”/count) * P(“people”/count) * P(“are”/count) * P(“in”/count) * P(“France”/count)$
Regardons maintenant chacune de ces expressions : $P(“How”/count)$ exprime la probabilité de rencontrer le mot “How” dans une question de catégorie count. Or, ce mot apparait 1 fois dans la catégorie, qui compte en tout 7 mots (on peut se référer au tableau présenté plus haut) : $P(“How”/count) = 1/7$
Le mot “many” apparait également une fois sur 7 : $P(“many”/count) = 1/7$
Le mot “people” n’apparait pas dans la catégorie count. On va associer aux mots hors catégorie une probabilité arbitrairement petite, mais non nulle, pour éviter que le produit final ne tombe à zéro. $P(“many”/count) = 10^{⁻3}$
Après avoir calculé la probabilité d’apparition de chaque mot, nous obtenons par leur produit le terme $P(“How\ many\ people\ are\ in\ France”/count)$. Il est égal à $(1/7)⁵ * 10^{⁻3} \approx 5,94 * 10^{⁻8}$
De la même manière, $P(“How\ many\ people\ are\ in\ France”/ind)= {10^{⁻3}}^6 = 10^{⁻18} $
Enfin, $P(“How\ many\ people\ are\ in\ France”/date)= 1/7 * {10^{⁻3}}^5 \approx 1,42 * 10^{⁻16} $
On peut noter que les probabilités caclulées sont directement dépendantes du nombre de termes de la phrase présents dans chaque catégorie : 5 mots de la phrase sur 6 sont présents dans la catégorie count, contre 0 dans ind et 1 dans date.
On peut ensuite remarquer que les probabilités $P(count)$, $P(date)$ et $P(ind)$ sont toutes égales à $1/3$
Dans l’expression $\frac{P(“How\ many\ people\ are\ in\ France”/ \textbf {categorie}) * P(\textbf {categorie})}{P(“How\ many\ people\ are\ in\ France”)} $, le seul terme non constant est celui que nous venons de calculer. C’est donc lui qui va determiner l’ordre de nos probabilités : $P(count/”How\ many\ people\ are\ in\ France”) > P(date/”How\ many\ people\ are\ in\ France”) > P(ind/”How\ many\ people\ are\ in\ France”)$
Notre phrase initiale a donc, selon notre modèle, plus de chances d’appartenir à la catégorie count.
C’est cette idée d’inférence bayésienne que nous allons utiliser pour construire notre classificateur, en prenant cette fois-ci l’intégralité des phrases de notre base TREC. On espère que la diversité des phrases présentes dans cette base contribuera à la robustesse de notre modèle.
Construction d’un classificateur bayésien
Nous allons diviser notre base de questions en deux. Une partie servira à entrainer notre modèle, et l’autre à évaluer ses performances. C’est une pratique courante qui évite d’évaluer un modèle sur une phrase sur laquelle il a été entrainé, chose qui biaiserait nos résultats.
#On importe de la librairie sklearn des fonctions utiles au comptage des mots.
from sklearn import feature_extraction, model_selection, naive_bayes, pipeline, manifold, preprocessing,feature_selection, metric
#On sépare notre base en deux
dtf_train, dtf_test = model_selection.train_test_split(data, test_size=0.3)
y_train = dtf_train["Category2"].values
corpus = dtf_train["Questions"] #ensemble des textes des questions d'entrainement
#On crée notre table d'occurence des mots dans chaque catégorie
vectorizer = feature_extraction.text.CountVectorizer(max_features=10000)#, ngram_range=(1,1))
vectorizer.fit(corpus)
classifier = naive_bayes.MultinomialNB()
X_train = vectorizer.transform(corpus)
model = pipeline.Pipeline([("vectorizer", vectorizer),
("classifier", classifier)])## train classifier
model["classifier"].fit(X_train, y_train)
X_test = dtf_test["Questions"].values
y_test = dtf_test["Category2"].values
predicted = model.predict(X_test)
predicted_prob = model.predict_proba(X_test)
metrics.accuracy_score(y_test, predicted) #0.4902200488997555
Notre classificateur a un taux de bonnes réponses d’environ 49%, ce qui est assez faible. Il faut cependant mettre ce résultat en perspective avec le fait que nous avons 50 catégories : le pur hasard nous donnerait un taux de réussite de 2% seulement.
Pour la classe 1, qui compte seulement 6 catégories, la précision est de 48,5%.
Une approche prenant en compte la structure du language : les word vectors
Notre modèle bayésien, s’il fait mieux que le pur hasard, possède une désavantage inhérent : Chaque apparition d’un mot est considérée comme indépendante des autres. Or, certains mots possèdent une proximité sémantique : les différentes conjuguaisons d’un même verbe, ou les noms de lieu, par exemple. Cette proximité n’est pas modélisée par notre approche, qui considère les mots comme des variables n’ayant aucun rapport entre elles.
Le concept d’embedding fait correspondre chaque mot à un point dans un espace continu, le plus souvent multidimensionnel. Voilà un exemple d’embeddings de 34 mots, en deux dimensions :
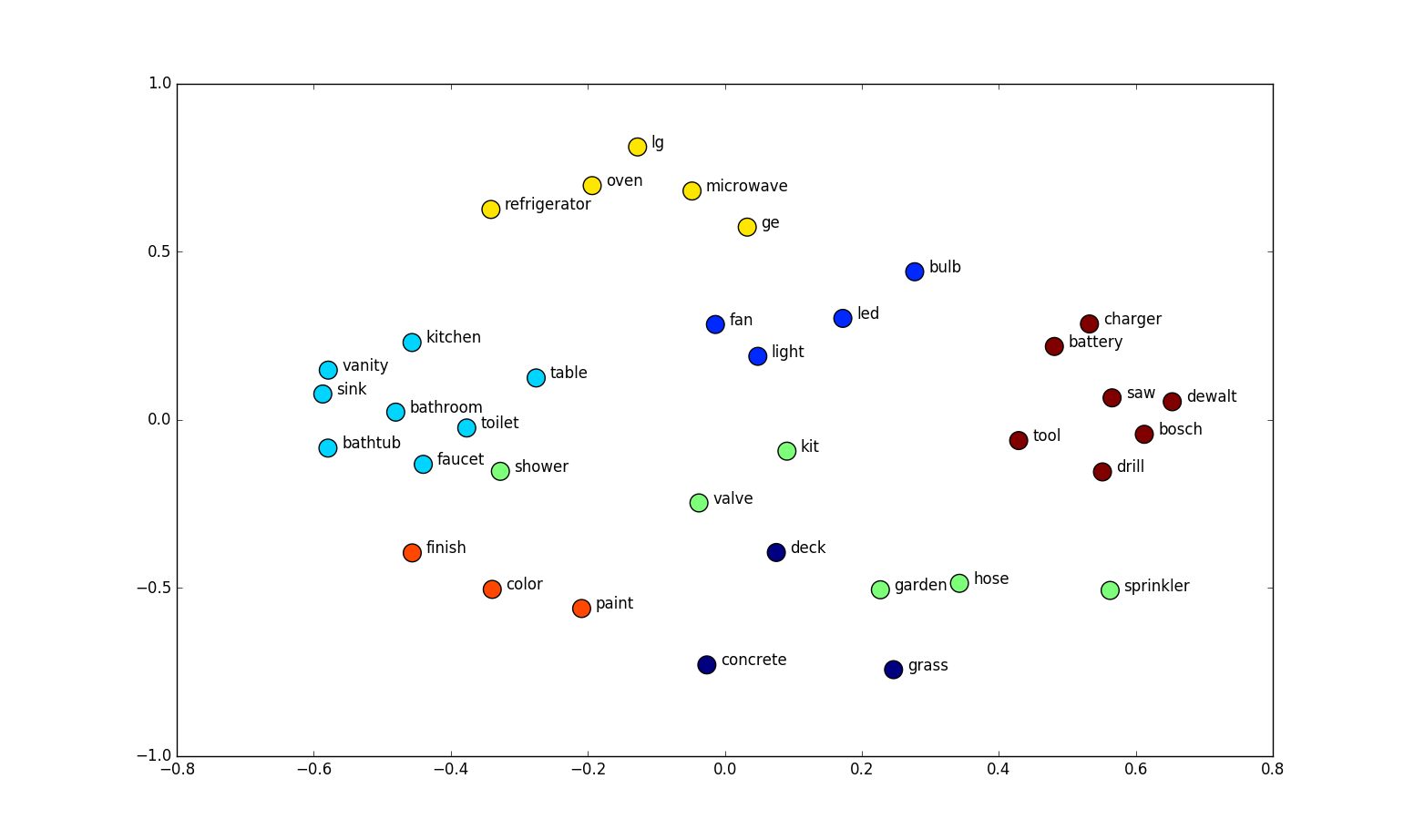
On remarque que les mots de sens proche sont souvent à coté, et qu’ils forment même des groupes sémantiques cohérents. Et c’est précisément pour ça que cette méthode est intéressante : elle permet de représenter la structure du language utilisé, et faciliter la tâche de certains algorithmes de traitement du language.
Mais alors, comment produire des embeddings ? La plupart des méthodes exploitent des corpus de textes existants. L’hypothèse de base de ces méthodes est que des mots qui apparaissent souvent dans des voisinages de mots similaires ont plus de chance de partager des attributs. Par exemple, les mots apparaisant après un pronom personnel ont de grandes chances d’être des verbes, les mots appartenant au même champ lexical on plus de chance d’être les uns à côté des autres, etc …
Nous allons tenter de construire nos propres embeddings, en suivant la méthode Continuous bag-of-words (CBOW), proposée par Mikolov. Cette méthode consiste à entrainer un réseau de neurones possédant une couche cachée à prédire un mot à partir de ses mots voisins.
Pour celà, on va exploiter notre base de données de questions. Notre réseau prendra en entrée un mot d’une question, et il devra correctement prédire un mot de son voisinage.
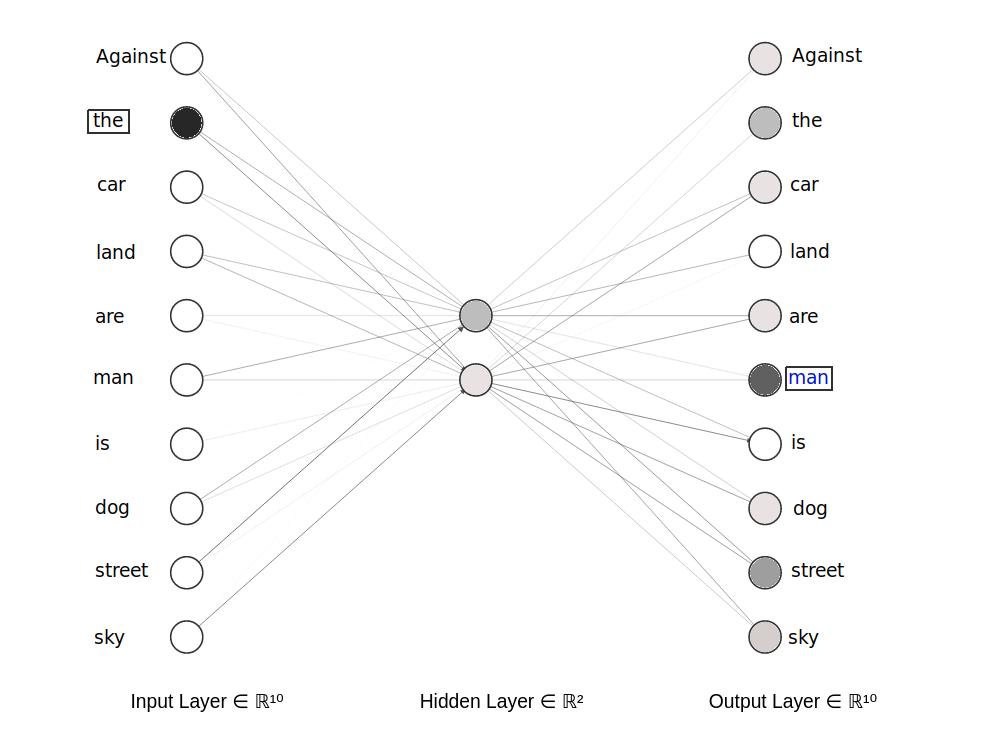
Une version simplifiée du modèle a été mise ci-dessus. On a en entrée le mot “the”: dans la couche d’entrée, le neurone correspondant à ce mot est activée. On va entrainer le réseau à prédire un mot voisin, ici le mot “man”.
A la fin de l’entrainement du réseau, on espère que les mots de sens similaires mèneront aux mêmes prédictions de mots voisins, et auront donc des activations de couche cachée similaires : c’est ces valeurs d’activations que nous considererons par la suite comme nos embeddings.
On adapte d’abord notre jeu de données pour qu’il soit lisible par le réseau : On va créer des paires de mots $(x,y)$, $y$ étant le mot à prédire, et $x$ un mot “voisin”. Nous considérons ici comme mot voisin de $y$ tout mot apparaissant dans la même phrase et éloigné de 4 mots au plus.
import itertools
import pandas as pd
import numpy as np
import re
import os
from tqdm import tqdm
# Drawing the embeddings
import matplotlib.pyplot as plt
# Deep learning:
from keras.models import Input, Model
from keras.layers import Dense
from scipy import sparse
texts = [x for x in data['Questions']]
# Defining the window for context
window = 4
import re
import numpy as np
def text_preprocessing(
text:list,
punctuations = r'''!()-[]{};:'"\,<>./?@#$%^&*_“~''',
stop_words = [ "a", "the" , "to" ]
)->list:
"""
A method to preproces text
"""
for x in text.lower():
if x in punctuations:
text = text.replace(x, "")
# Removing words that have numbers in them
text = re.sub(r'\w*\d\w*', '', text)
# Removing digits
text = re.sub(r'[0-9]+', '', text)
# Cleaning the whitespaces
text = re.sub(r'\s+', ' ', text).strip()
# Setting every word to lower
text = text.lower()
# Converting all our text to a list
text = text.split(' ')
# Droping empty strings
text = [x for x in text if x!='']
# Droping stop words
text = [x for x in text if x not in stop_words]
return text
def word_count(str):
counts = dict()
words = str.split()
for word in words:
if word in counts:
counts[word] += 1
else:
counts[word] = 1
return counts
word_lists = []
all_text = []
for text in texts:
# Cleaning the text
text = text_preprocessing(text)
# Appending to the all text list
all_text += text
# Creating a context dictionary
for i, word in enumerate(text):
for w in range(window):
# Getting the context that is ahead by *window* words
if i + 1 + w < len(text):
word_lists.append([word] + [text[(i + 1 + w)]])
# Getting the context that is behind by *window* words
if i - w - 1 >= 0:
word_lists.append([word] + [text[(i - w - 1)]])
frequencies = {}
for item in all_text:
if item in frequencies:
frequencies[item] += 1
else:
frequencies[item] = 1
word_lists est une liste des paires (mot voisin, mot à prédire) trouvées dans le texte. On y enlever les mots trop peu communs, susceptibles de perturber la performance du modèle :
word_lists = [item for item in word_lists if frequencies[item[0]]>20 and frequencies[item[1]]>20]
On va ensuite créer deux vecteurs, X et Y, contenant respectivement la liste des mots voisins et des mots à prédire, encodés sous forme one-hot. Celà signifie que chaque vecteur est de taille N (= taille du vocabulaire total) et contient un 1 à la position correspondant au mot codé, le reste du vecteur étant à zéro.

dict_short = {}
j = 0
for i, word in enumerate(word_lists):
if word[0] not in dict_short :
dict_short.update({ word[0]: j })
j=j+1
n_words_short = len(dict_short)
# Creating the X and Y matrices using one hot encoding
X = []
Y = []
words = list(dict_short.keys())
for i, word_list in tqdm(enumerate(word_lists)):
# Getting the indices
main_word_index = dict_short.get(word_list[0])
context_word_index = dict_short.get(word_list[1])
# Creating the placeholders
X_row = np.zeros(n_words_short)
Y_row = np.zeros(n_words_short)
# One hot encoding the main word
X_row[main_word_index] = 1
# One hot encoding the Y matrix words
Y_row[context_word_index] = 1
# Appending to the main matrices
X.append(X_row)
Y.append(Y_row)
Le format des objets X et Y nous permet maintenant d’entrainer un réseau de neurones :
import tensorflow as tf
model = tf.keras.Sequential([
tf.keras.layers.Dense(2, activation='softmax'),
tf.keras.layers.Dense( n_words_short) #(len(unique_word_dict))
])
model.compile(loss = 'categorical_crossentropy', optimizer = 'adam')
model.fit(x=np.array(X), y=np.array(Y), epochs=10)
On peut maintenant visualiser nos embeddings en 2 dimensions :
import random
weights = model.get_weights()[0]
# Creating a dictionary to store the embeddings in. The key is a unique word and
# the value is the numeric vector
embedding_dict = {}
for word in words:
embedding_dict.update({
word: weights[dict_short.get(word)]
})
# Ploting the embeddings
plt.figure(figsize=(10, 10))
for word in list(dict_short.keys()):
coord = embedding_dict.get(word)
plt.scatter(coord[0], coord[1])
plt.annotate(word, (coord[0], coord[1]))
On peut remarquer que plusieurs mots apparentés sont relativement proches (dog/animal, day/year, city/capital). Mais il est difficile d’y trouver un cohérence globale.
On peut également créer des embeddings de dimensions supérieures : Pour ça, on doit changer la taille de la couche cachée de notre réseau. Une plus grande dimension d’embeddings permet au réseau de former des structures sémantiques plus complexes entre les différents mots. Voilà des embeddings entrainés sur le même texte, mais en 3 dimensions :
Ici aussi, on remarque des similarités entre des mots proches. On va tenter de se servir de notre structure d’embeddings pour classifier nos questions.
Utilisation des word vectors pour notre classification
Dans le même esprit que les word embeddings, plusieurs travaux se penchent sur les embeddings de phrases, et sur la possibilité de saisir leur sens à travers des vecteurs. Arora et al. décrivent plusieurs méthodes pour créer ces embeddings de phrases, mais soulignent aussi que la méthode consistant à prendre la moyenne des embeddings des mots de la phrase donne des résultats satisfaisants. C’est ce qu’on va essayer ici :
def sentence_mean(sentence):
array_vect = [np.array([0,0,0])]
for i in range(len(sentence)):
if sentence[i] in embedding_dict.keys():
array_vect.append(embedding_dict[sentence[i]])
#else :
# array_vect.append(np.array([0,0,0]))
return np.array(sum(array_vect)/max(1,len(array_vect)))
from nltk.tokenize import word_tokenize
data['processed_text'] = data["Questions"].str.lower().replace(r"[^a-zA-Z ]+", "")
data['vec'] = data['processed_text'].apply(lambda x: word_tokenize(x))
data['mean_vec'] = data['vec'].apply(lambda x: sentence_mean(x))
data['x'] = data['mean_vec'].apply(lambda x: x[0])
data['y'] = data['mean_vec'].apply(lambda x: x[1])
data['z'] = data['mean_vec'].apply(lambda x: x[2])
On a associé ici à chaque question la moyenne des embeddings 3d des mots qui la composent. On peut donc sur un graphique associer un point à chaque phrase :
On a aussi affiché les catégories des questions, avec des couleurs différentes. Il serait illisible d’afficher les 50 sous-catégories, on montre donc les 6 catégories de premier niveau. (Abbreviation, Description and abstract concepts, Entities, Human beings, Locations et Numeric values).
Il n’y a pas de séparation marquée entre les catégories, mais on peut déja remarquer des agglomérations de phrases de même catégorie à certains endroits. Si les groupes étaient plus marqués, ce serait alors plus facile de classifier une phrase en fonction du groupe de points auquel son embedding appartient.
Pour affiner notre outil de classification, on va utiliser des word embeddings de mots plus performants, car déja entrainés sur un corpus beaucoup plus large : les Glove.
Ces vecteurs sont produits de la même manière qu’expliquée précédemment, mais sont de dimension 50, et sont entrainées la totalité du contenu anglais de wikipédia (2014), un corpus d’1,6 milliards de mots.
import gensim.downloader
glove_model = gensim.downloader.load('glove-wiki-gigaword-50')
def sentence_mean_glove(sentence):
array_vect = []
for i in range(min(4,len(sentence))):
if sentence[i] in glove_model.key_to_index.keys():
array_vect.append(glove_model[sentence[i]])
return sum(array_vect)/len(array_vect)
data['mean_vec_glove'] = data['vec'].apply(lambda x: sentence_mean_glove(x))
Chaque question est maintenant représentée par un vecteur de taille 50. Pour pouvoir visualiser ces vecteurs, nous allons réduire leurs dimensions avec l’algorithme t-sne :
from sklearn.manifold import TSNE
sentence_vec_tsne = TSNE(n_components=3).fit_transform(data['mean_vec_glove'].tolist())
On peut maintenant afficher notre nuage de points :
import plotly.graph_objects as go
fig = go.Figure(data=[go.Scatter3d(
x=[a[0] for a in sentence_vec_tsne], # ie [0, 1, 2, 3]
y=[a[1] for a in sentence_vec_tsne], # ie [0, 1, 2, 3]
z=[a[2] for a in sentence_vec_tsne], # ie [0, 1, 2, 3]
hovertemplate='<b>%{text}</b><extra></extra>',
text = data["Questions"],
mode='markers',
marker=dict(
size=3,
opacity=0.8,
color=data['Category1'].map(col_dict),
)
)])
fig.show()
On peut remarquer que les groupes sont bien plus marqués. On va se servir de ces groupements pour construire un classificateur. Le principe est simple : Pour une question donnée, on va calculer son sentence embedding, et l’associer à la classe de la question connue la plus proche :
X = data['mean_vec_glove'].tolist()
y = data['Category2'].tolist()
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.4, random_state=42)
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=1)
neigh.fit(X_train, y_train)
score = neigh.score(X_test, y_test)
score
Le score de classification est cette fois-ci de 0.675 pour la classe 1 (pour rappel, 6 catégories), et 0.567 pour la catégorie 2 (50 catégories). Il est encore assez bas vis-à-vis de l’état de l’art en classification, mais déja supérieur à notre précédente méthode.
On remarque quand même qu’au delà de la classification, nos embeddings ont réussi a modéliser la sémantique de nos questions : les phrases voisines ont systématiquement un sens proche. Ce modèle pourrait servir comme moteur de recherche dans des domaines où la sémantique des phrases est importante, comme par exemple la recherche de questions similaires sur un forum d’entraide.
Pour améliorer encore notre classificateur, on pourrait notamment utiliser des méthodes plus sophistiquées que la moyenne pour nos sentences embeddings :Conneau et al. proposent l’utilisation de réseaux récurrents pour capturer le sens de l’ensemble des embeddings des mots d’une phrase, de manière similaire à ce qui est fait dans cet article portant sur la description d’images.
Cer et al. proposent quand à eux deux méthodes, l’une basée sur la convolution, dont on parle également ici, et l’autre basée sur les transformers, des réseaux basés sur l’attention, et dont on parlera peut être prochainement.
Le code utilisé dans cet article est disponible ici.